树的定义及描述

树（Tree）是由 n 个结点构成的有限集合。当 n=0 时，称为空树；对于任意一颗非空树，它具备以下特征：

• 树中有一个称为根的特殊节点，用 r 表示；
• 其余结点可分为 m 个互不相交的有限集 T1,T2,…,Tm，其中的每个集合本身又是一棵树，称为原来树的子树。

树的特点：

• 子树是不相交的；
• 除了根节点外，每个结点有且仅有一个父节点；
• 一颗 N 个结点的树有 N-1 条边。

树的一些基本术语：

1.结点的度（Degree）：结点的子树个数
2.树的度：树的所有结点中最大的度数
3.叶结点（Leaf）：度为 0 的结点
4.父节点（Parent）：有子树的结点是其子树的根结点的父节点
5.子节点（Child）：若 A 结点是 B 结点的父节点，则称 B 结点是 A 结点的子节点；子节点也称孩子结点
6.兄弟节点（Sibling）：具有同一父节点的各节点彼此是兄弟节点
7.结点的层次（Level）：规定根节点在 1 层，其它任一结点的层次是其父节点层数加1
7.树的深度（Depth）：树中所有结点中的最大层次是这棵树的深度

二叉树

二叉树的定义

二叉树是一个有穷的结点集合。这个集合可以为空，若不为空，则它是由根节点和称为其左子树和右子树的两个互不相交的二叉树组成。一般来讲二叉树有以下 5 种基本形态：

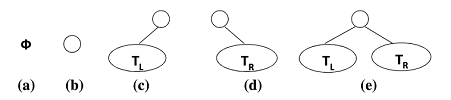
需要注意的是二叉树的子树有左右顺序之分。

特殊的二叉树：

• 斜二叉树
• 完美二叉树或满二叉树
• 完全二叉树

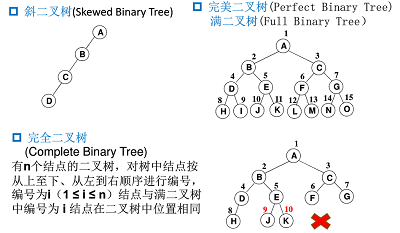
二叉树的性质

• 二叉树第 i 层的最大结点数为 2^(i-1), i>= 1
• 深度为 k 的二叉树有最大结点数 2^k - 1, k>=1
• 对任何非空的二叉树，若 n0 表示叶结点个数、n2 是度为 2 的非叶结点个数，则有 n0 = n2 + 1。
  以下是证明：
  设 n1 表示度为 1 的结点个数，则二叉树的总结点个数为 n0 + n1 + n2;
  二叉树的边数为 2n2 + n1，总结点数等于边数 + 1；
  因此：n0 + n1 + n2 = 2n2 + n1 + 1
  所以 n0 = n2 + 1。

二叉树的存储结构

1.顺序存储

完全二叉树：按从上到下，从左到右顺序存储 n 个结点的完全二叉树的结点父子关系

• 非根节点的父节点的序号是 [i/2];
• 结点为 i 的左孩子结点序号为 2i；
• 结点为 i 的右孩子结点序号为 2i+1;

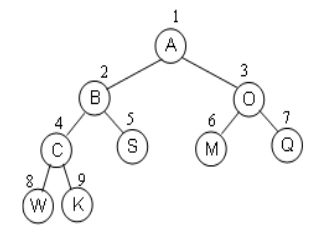
一般二叉树如果采用这种结构可能造成极大的空间浪费，因此可采用链式存储结构。

2.链式存储

以下是二叉树的链式存储结构示意图：

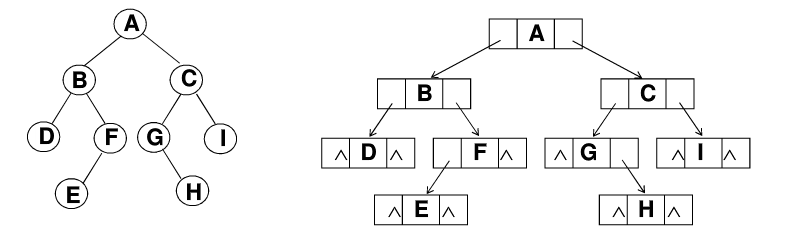
因此可以用以下代码来表示如上结构：

typedef int ElementType;

typedef struct TreeNode* BinTree;
struct TreeNode {
    ElementType Data;
    BinTree Left;
    BinTree Right;
};

二叉树的递归遍历

1.先序遍历

遍历过程为：

• 访问根节点
• 先序遍历其左子树
• 先序遍历其右子树

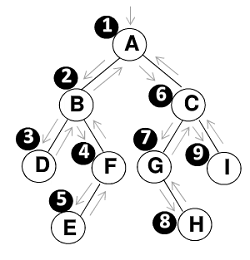
void PreOrderTraversal(BinTree BT) {
    if(BT) {
        printf("%d ",BT->Data);
        PreOrderTraversal(BT->Left);
        PreOrderTraversal(BT->Right);
    }
}

2.中序遍历

遍历过程为：

• 中序遍历其左子树
• 访问根节点
• 中序遍历其右子树

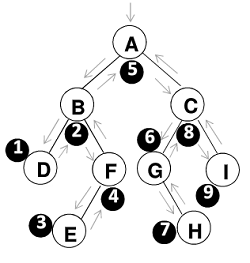
void InOrderTraversal(BinTree BT) {
    if(BT) {
        InOrderTraversal(BT->Left);
        printf("%d ",BT->Data);
        InOrderTraversal(BT->Right);
    }
}

3.后序遍历

遍历过程为：

• 后序遍历其左子树
• 后序遍历其右子树
• 访问根节点

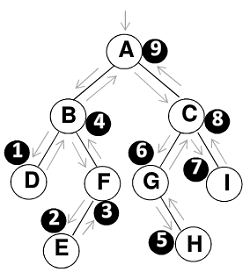
void PostOrderTraversal(BinTree BT) {
    if(BT) {
        PostOrderTraversal(BT->Left);
        PostOrderTraversal(BT->Right);
        printf("%d ",BT->Data);
    }
}

先序、中序、后序遍历过程：遍历过程中经过结点的路线一样，只是访问各节点的时机不同。先序是第一次经过该结点就访问，中序是第二次经过该结点访问，后序是第三次经过该结点访问。

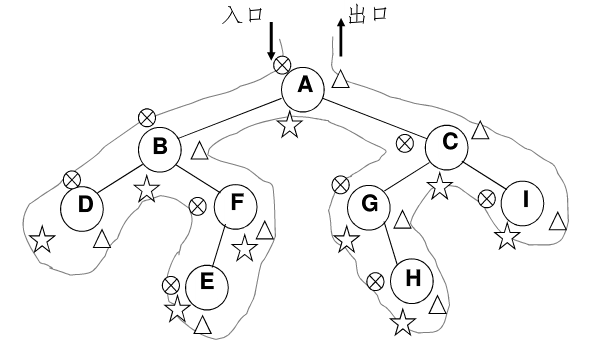
二叉树的非递归遍历

二叉树先序、中序、后序遍历的非递归算法实现的基本思路：使用堆栈。

1.先序遍历的非递归算法

• 遇到一个结点访问之，并将其压入堆栈，再去访问它的左子树
• 左子树遍历结束之后，从栈顶弹出一个结点
• 然后再去先序遍历弹出结点的右子树

void PreOrderTraversal(BinTree BT) {
    BinTree T = BT;
    Stack S = CreateStack(MaxSize); /* 初始化堆栈 */
    while(T || !Empty(S)) { /* 如果树不为空或者堆栈不为空 */

        while(T) {
            /* 遇到一个结点访问之，并将其压入堆栈，再去访问它的左子树 */
            printf("%d ",T->Data);
            Push(S,T);
            T = T->Left;
        }
        if(!Empty(S)) {
            /* 左子树遍历完之后，弹出栈顶元素，并遍历其右子树 */
            T = Pop(S);
            T = T->Right;
        }
    }
}

2.中序遍历的非递归算法

• 遇到一个结点将其压入堆栈，并去访问它的左子树
• 当左子树遍历结束之后，从栈顶弹出这个结点并访问它
• 然后再去中序遍历弹出结点的右子树。

void InOrderTraversal(BinTree BT) {
    BinTree T = BT;
    Stack S = CreateStack(MaxSize); /* 初始化堆栈 */
    while(T || !Empty(S)) { /* 如果树不为空或者堆栈不为空 */

        while(T) {
            /* 遇到一个结点将其压入堆栈并去访问它的左子树 */
            Push(S,T);
            T = T->Left;
        }
        if(!Empty(S)) {
            /* 左子树遍历完之后，弹出栈顶元素，并访问其右子树 */
            T = Pop(S);
            printf("%d ",T->Data);
            T = T->Right;
        }

    }
}

3.后序遍历的非递归算法

• 遇到一个节点将其压入堆栈，再访问它的左子树
• 左子树遍历结束之后，弹出栈顶结点
  如果该结点有右节点且右节点还未被打印出栈，将该结点再次压入堆栈，后序遍历该结点的右子树
  如果该结点没有右结点或者该结点的右结点被访问过了，则访问该结点

void PostOrderTraversal(Bintree BT) {
    Bintree T = BT;
    Bintree PrintedRT = NULL;//上一个被打印出的右节点
    Stack S = CreateStack(Maxsize);
    while (T || !IsEmpty(S)) {
        while (T) {
            Push(S, T);
            T = T->left;
        }
        if (!IsEmpty(S)) {
            T = Pop(s);
            if ((T-> Right== NULL)||(T->Right == PrintedRT)) {    //右节点为空 或 右节点已经出栈
                printf("%d", T->Data);
                PrintedRT = T; //记录“上一个被打印出的右节点”
            }
            else {//有右节点且右节点还未被打印出栈
                Push(S, T);  //因为当前节点已经出栈，但右儿子节点还未先出栈，所以先把他压进去
                T = T->Right;  //转向右子树，进入下一次循环
            }
        }
    }
}

4.二叉树的层序遍历

二叉树的层序遍历的关键是使用 队列。

• 根结点入队
• 如果队列不为空，从中取出一个元素，并访问之，将其左右儿子顺序入队
• 重复第二步

void LevelOrderTraversal(BinTree BT) {

    if(!BT) return;

    BinTree T = BT;
    Queue Q = CreateQueue(MaxSize);

    AddQ(Q,T);

    while(!Empty(Q)) {
        T = DeleteQ(Q);
        printf("%d ",T->Data);
        if(T->Left) AddQ(Q,T->Left);
        if(T->Right) AddQ(Q,T->Right);
    }
}

遍历二叉树的应用

1.输出所有叶子结点

核心：叶子节点的左右儿子都为空

void PostOrderTraversal(BinTree BT) {
    if(BT) {
        PostOrderTraversal(BT->Left);
        PostOrderTraversal(BT->Right);
        if(!BT->Left && !BT->Right)
            printf("%d ",BT->Data);
    }
}

2.求二叉树的高度

int getHeight(BinTree BT) {
    int HL,HR,MaxH;
    if(BT) {
        HL = getHeight(BT->Left);
        HR = getHeight(BT->Right);
        MaxH = HL > HR ? HL : HR;
        return MaxH + 1;
    }
    else return 0;
}

3.由两种遍历确定一颗二叉树

由先序和中序遍历序列、后序和中序遍历序列可以唯一确定一棵二叉树。