二叉搜索树始终特殊的二叉树,它主要用于解决动态查找问题,能够比较快速地查找出想要的元素.而平衡二叉树是对二叉搜索树的改进,它本身也是一颗平衡二叉树,它保证查找所有结点的比较次数的平均值即树的“平均查找长度”最小.
二叉搜索树
查找问题可分为静态查找和动态查找,静态查找可以用二分查找算法,针对动态查找,数据应该如何组织呢?
二叉搜索树的定义
二叉搜索树(Binary Search Tree)也叫二叉排序树或二叉查找树,它是一种对排序和查找都很有用的特殊二叉树。一个二叉搜索树是一颗二叉树,它可以为空,如果不为空,它将满足以下性质:
非空左子树的所有值小于其根节点的值
非空右子树的所有值大于其根节点的值
左、右子树都是二叉搜索树
由于二叉搜索树具有左小右大的特点,因此对它进行中序遍历,将得到一个从小到大的输出序列。
二叉搜索树的动态查找
二叉搜索树的抽象数据结构定义与普通二叉树基本相同,只是多个以下几个特别的函数:
1.Position Find(BinTree BST, ElementType X):从二叉搜索树 BST 中查找元素 X,并返回其地址;
2.Position FindMin(BinTree BST):查找并返回最小值的地址;
3.Position FindMax(BinTree BST):查找并返回最大值的地址。
二叉搜索树的查找操作 Find
1.查找从根节点开始,如果树为空返回 NULL,表示未找到
2.如果不为空,则将根节点与 X 进行比较,根据比较结果进行不同的处理:
- 若 X 大于根节点的值,则在右子树中查找
- 若 X 小于根节点的值,则在左子树中查找
- 相等表示找到了,返回此结点
以下是找到的递归算法:
1 | Position Find(BinTree BST, ElementType X) { |
以下是查找的非递归算法:
1 | Position Find(BinTree BST, ElementType X) { |
查找最大值和最小值
根据二叉搜索树的性质,最小值一定在二叉搜索树的最左分支的端点上,而最大值一定在最右分支的端点上。
以下是分别使用递归算法和非递归算法实现的查找最大值和最小值。
1 | Position FindMax(BinTree BST) { |
二叉搜索树的插入
将元素 X 插入二叉搜索树 BST 中关键是找到元素插入的位置。
1 | BinTree Insert(BinTree BST,ElementType X) { |
二叉搜索树的删除
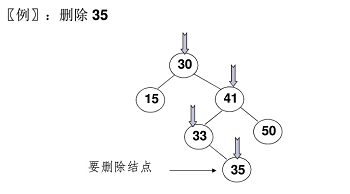
考虑三种情况:
要删除的是叶结点:直接删除,并修改其父节点指针——置为 NULL
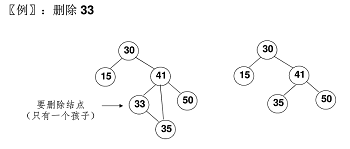
要删除的结点只有一个孩子节点:将其父节点的指针指向要删除结点的孩子节点
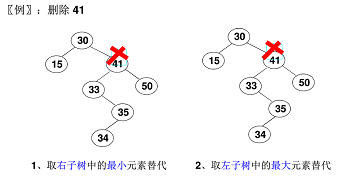
要删除结点有左、右两颗子树:用另一结点替换被删除结点:右子树中最小元素 或 左子树中最大元素
1 | BinTree Delete(BinTree BST, ElementType X) { |
平衡二叉树
对于二叉搜索树进行查找的时间复杂度是由是由查找过程中的比较次数来衡量的,比较是从根结点到叶结点的路径进行的,它取决于树的深度。树深在最好情况下是 logN,所以二叉搜索树在最好情况的查找复杂度是 O(logN)。但这一结论是由完全二叉树导出的,事实上 N 个结点的二叉树深度取决于其树枝的分布情况。当二叉树退化为一颗单枝树的极端情况下,查找时间复杂度将是线性的 O(N)。
假定二叉树中每个结点的查找概率都是相同的,我们称查找所有结点的比较次数的平均值为树的“平均查找长度”(Average Search Length,ASL)。如下图所示,可以得到各二叉树的平均查找长度:
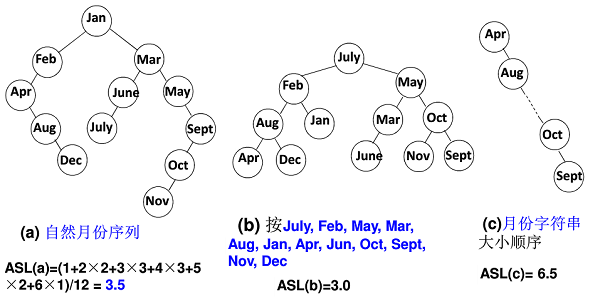
上述示例表明,一棵树的 ASL 值越小,它的结构越好,与完全二叉树越接近,对它的查找时间复杂度也越接近 O(logN)。因此为了保证二叉树查找的对数级查找时间效率。设计出了平衡二叉树这一数据结构。
平衡二叉树的定义
平衡二叉树又称 AVL 树,它也是一颗二叉搜索树。
定义:AVL树是一颗空树或者是具有以下性质的非空二叉搜索树:
1.任一结点的左右子树均为 AVL 树;
2.根结点左右子树的高度差的绝对值不超过 1。
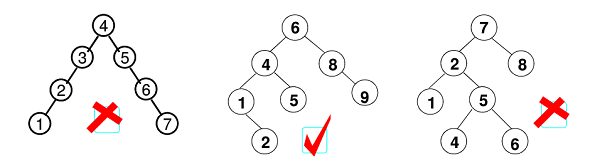
定义:对于二叉树中的任一结点 T,其平衡因子(Balance Factor,BF)定义为 BF(T) = hL - hR,其中 hL 和 hR 分别为左右子树的高度。
因此根结点左右子树的高度差的绝对值不超过 1 可以量化为 |BF(T)| <= 1。
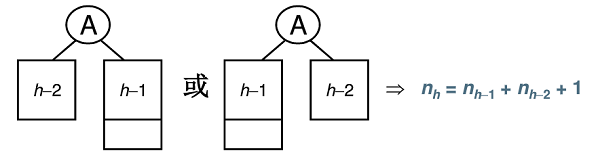
设高度(边的长度)为 h 的平衡二叉树的最少结点数为 nh,则有:
h = 0, n0 = 1
h = 1, n1 = 2
h = 2, n2 = 4
h = 3, n3 = 7
…
依次类推可以得到:nh = n(h-1) + n(h-2) + 1;
求高度(边的长度)为 h 的平衡二叉树的最少结点数要么左边少一层要么右边少一层,因此高度(边的长度)为 h 的平衡二叉树的最少结点数 nh 等于高度(边的长度)为 h-1 的平衡二叉树的最少结点数 + 高度(边的长度)为 h-2 的平衡二叉树的最少结点数。
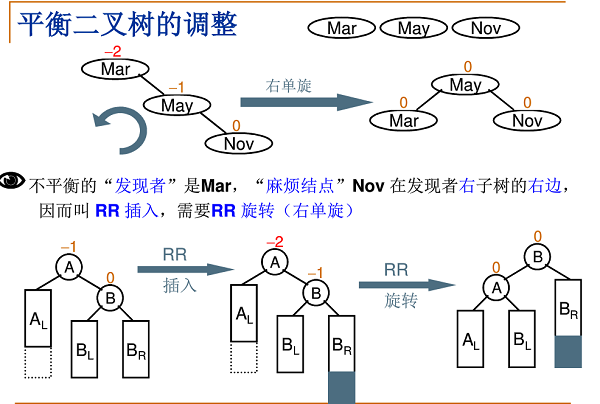
平衡二叉树的调整
1.右单旋
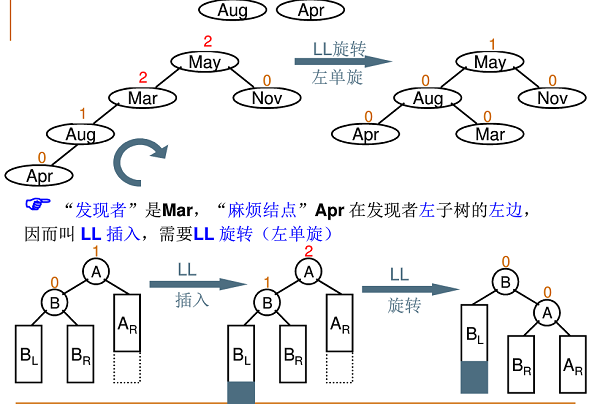
2.左单旋
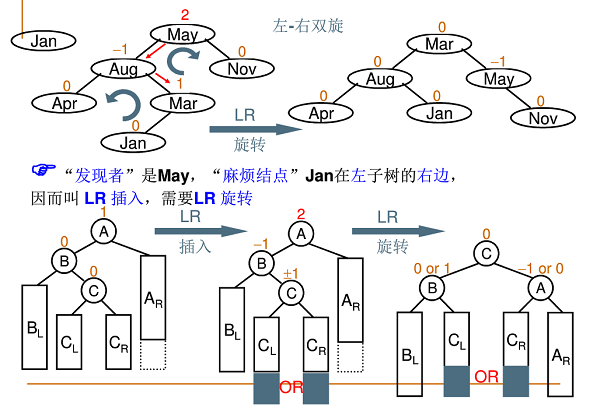
3.左-右双旋
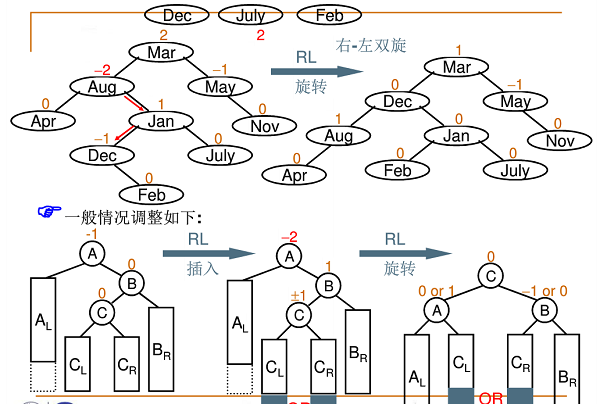
4.右-左双旋